Վիքիպեդիա

Հանրային բանալիների գաղտնագրություն

Հանրային բանալիների գաղտնագրություն կամ ասիմետրիկ ծածկագրություն, ծածկագրային համակարգերի ոլորտն է, որն օգտագործում է հարակից բանալիների զույգեր։ Յուրաքանչյուր բանալի զույգ բաղկացած է հանրային բանալիից և համապատասխան մասնավոր բանալիից[1]։ Բանալիների զույգերը ստեղծվում են գաղտնագրման ալգորիթմներով, որոնք հիմնված են մաթեմատիկական խնդիրների վրա, որոնք կոչվում են միակողմանի ֆունկցիաներ։ Հանրային բանալիների ծածկագրման անվտանգությունը կախված է մասնավոր բանալին գաղտնի պահելուց։ Հանրային բանալին կարող է բաց բաշխվել՝ չվտանգելով անվտանգությունը[2]։

Անկանխատեսելի (սովորաբար մեծ և պատահական) թիվ օգտագործվում է ընդունելի զույգ ստեղների ստեղծումը սկսելու համար, որը հարմար է ասիմետրիկ բանալիների ալգորիթմի կողմից օգտագործելու համար:
Ասիմետրիկ բանալիների գաղտնագրման սխեմայում յուրաքանչյուրը կարող է գաղտնագրել հաղորդագրությունները՝ օգտագործելով հանրային բանալի, բայց միայն զուգակցված մասնավոր բանալի կրողը կարող է վերծանել այդպիսի հաղորդագրությունը: Համակարգի անվտանգությունը կախված է մասնավոր բանալիի գաղտնիությունից, որը չպետք է հայտնի դառնա որևէ մեկին:
Diffie-Hellman բանալիների փոխանակման սխեմայում յուրաքանչյուր կողմ ստեղծում է հանրային/մասնավոր բանալիների զույգ և բաշխում է այդ զույգի հանրային բանալին: Միմյանց հանրային բանալիների վավերական (սա կարևոր է) պատճեն ստանալուց հետո Ալիսն ու Բոբը կարող են օֆլայն հաշվարկել ընդհանուր գաղտնիքը: Ընդհանուր գաղտնիքը կարող է օգտագործվել, օրինակ, որպես սիմետրիկ ծածկագրի բանալին, որը, ըստ էության, բոլոր դեպքերում շատ ավելի արագ կլինի:
Այս օրինակում հաղորդագրությունը թվային ստորագրված է Ալիսի անձնական բանալիով, սակայն հաղորդագրությունն ինքնին գաղտնագրված չէ: 1) Ալիսը ստորագրում է հաղորդագրություն իր անձնական բանալիով: 2) Օգտագործելով Ալիսի հանրային բանալին՝ Բոբը կարող է ստուգել, որ Ալիսն ուղարկել է հաղորդագրությունը, և որ հաղորդագրությունը փոփոխված չէ:

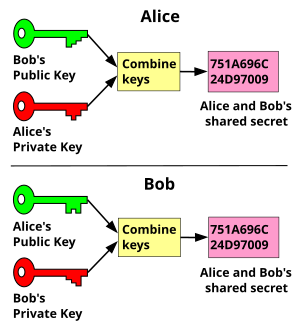
Հանրային բանալիով գաղտնագրման համակարգում ցանկացած ոք, ով ունի հանրային բանալի, կարող է գաղտնագրել հաղորդագրությունը՝ ստանալով գաղտնագրված տեքստ, բայց միայն նրանք, ովքեր գիտեն համապատասխան մասնավոր բանալին, կարող են վերծանել գաղտնագրված տեքստը՝ սկզբնական հաղորդագրությունը ստանալու համար[3]։

Օրինակ, լրագրողը կարող է հրապարակել գաղտնագրման բանալիների զույգի հանրային բանալին վեբ կայքում, որպեսզի աղբյուրները կարողանան գաղտնի հաղորդագրություններ ուղարկել լրատվական կազմակերպությանը ծածկագրված տեքստով։ Միայն լրագրողը, ով գիտի համապատասխան անձնական բանալին, կարող է գաղտնագրել գաղտնագրված տեքստերը՝ աղբյուրների հաղորդագրությունները ստանալու համար։ Գաղտնալսողը, որը կարդում է էլեկտրոնային նամակը լրագրողին տանող ճանապարհին, չի կարող վերծանել գաղտնագրված տեքստերը։ Այնուամենայնիվ, հանրային բանալիների գաղտնագրումը չի թաքցնում մետատվյալները, ինչպես օրինակ, թե ինչ համակարգիչ է օգտագործել աղբյուրը հաղորդագրություն ուղարկելու համար, երբ են ուղարկել այն կամ որքան երկար է։ Հանրային բանալիների կոդավորումն ինքնին նույնպես ոչինչ չի ասում ստացողին այն մասին, թե ով է ուղարկել հաղորդագրություն, այն պարզապես թաքցնում է հաղորդագրության բովանդակությունը գաղտնագրված տեքստում, որը կարող է վերծանվել միայն մասնավոր բանալիով։

Թվային ստորագրության համակարգում ուղարկողը կարող է ստորագրություն ստեղծելու համար օգտագործել անձնական բանալի և հաղորդագրություն։ Յուրաքանչյուր ոք, ով ունի համապատասխան հանրային բանալի, կարող է ստուգել, թե արդյոք ստորագրությունը համընկնում է հաղորդագրության հետ, բայց կեղծարարը, ով չգիտի մասնավոր բանալին, չի կարող գտնել որևէ հաղորդագրության/ստորագրության զույգ, որը ստուգում կանցնի հանրային բանալիով[4][5]։

Օրինակ, ծրագրային ապահովման հրատարակիչը կարող է ստեղծել ստորագրության բանալիների զույգ և ներառել հանրային բանալին համակարգիչների վրա տեղադրված ծրագրաշարի մեջ։ Հետագայում հրատարակիչը կարող է թարմացում տարածել մասնավոր բանալիով ստորագրված ծրագրաշարի վրա, և թարմացում ստացող ցանկացած համակարգիչ կարող է հաստատել դրա իսկականությունը՝ հաստատելով ստորագրությունը՝ հանրային բանալին օգտագործելով։ Քանի դեռ ծրագրաշարի հրատարակիչը գաղտնի է պահում անձնական բանալին, նույնիսկ եթե կեղծարարը կարող է վնասակար թարմացումներ տարածել համակարգիչների վրա, նրանք չեն կարող համոզել համակարգիչներին, որ ցանկացած վնասակար թարմացում իրական է։

Հանրային բանալիների ալգորիթմները ժամանակակից կրիպտոհամակարգերում անվտանգության հիմնարար պրիմիտիվներն են, ներառյալ հավելվածներն ու արձանագրությունները, որոնք ապահովում են էլեկտրոնային հաղորդակցության և տվյալների պահպանման գաղտնիությունը, իսկությունը և անհերքելիությունը։ Դրանք հիմնված են բազմաթիվ ինտերնետային ստանդարտների վրա, ինչպիսիք են Transport Layer Security (TLS), SSH, S/MIME և PGP: Որոշ հանրային բանալիների ալգորիթմներ ապահովում են բանալիների բաշխում և գաղտնիություն (օրինակ՝ Diffie–Hellman բանալիների փոխանակում), ոմանք ապահովում են թվային ստորագրություններ (օրինակ՝ թվային ստորագրության ալգորիթմ), իսկ ոմանք ապահովում են երկուսն էլ (օրինակ՝ RSA): Համեմատած սիմետրիկ կոդավորման հետ՝ ասիմետրիկ գաղտնագրումը բավականին դանդաղ է, քան լավ սիմետրիկ գաղտնագրումը, շատ նպատակների համար չափազանց դանդաղ[6]։ Այսօրվա կրիպտոհամակարգերը (օրինակ՝ TLS-ը, Secure Shell-ը) օգտագործում են և՛ սիմետրիկ կոդավորումը, և՛ ասիմետրիկ կոդավորումը, հաճախ ասիմետրիկ կոդավորումը օգտագործելով գաղտնի բանալի ապահով փոխանակման համար, որն այնուհետև օգտագործվում է սիմետրիկ գաղտնագրման համար։

Նկարագրություն

խմբագրել

Մինչև 1970-ականների կեսերը բոլոր գաղտնագրային համակարգերը օգտագործում էին սիմետրիկ բանալի ալգորիթմներ, որոնցում նույն գաղտնագրային բանալին օգտագործվում է հիմքում ընկած ալգորիթմի հետ ինչպես ուղարկողի, այնպես էլ ստացողի կողմից, որոնք երկուսն էլ պետք է գաղտնի պահեն այն։ Անհրաժեշտ է, որ յուրաքանչյուր նման համակարգի բանալին նախապես պետք է փոխանակվեր հաղորդակցվող կողմերի միջև ինչ-որ ապահով ձևով, նախքան համակարգի ցանկացած օգտագործումը, օրինակ՝ ապահով ալիքի միջոցով։ Այս պահանջը երբեք աննշան չէ և շատ արագ դառնում է անկառավարելի, քանի որ մասնակիցների թիվը մեծանում է, կամ երբ ապահով ալիքները հասանելի չեն, կամ երբ (ինչպես խելամիտ կրիպտոգրաֆիկ պրակտիկա) բանալիները հաճախ փոխվում են։ Մասնավորապես, եթե հաղորդագրությունները նախատեսված են այլ օգտատերերից անվտանգ լինելու համար, յուրաքանչյուր հնարավոր զույգ օգտագործողների համար անհրաժեշտ է առանձին բանալի։

Ի հակադրություն, հանրային բանալիների համակարգում հանրային բանալիները կարող են լայնորեն և բաց տարածվել, և միայն համապատասխան մասնավոր բանալիները պետք է գաղտնի պահվեն դրա տիրոջ կողմից։

Հանրային բանալիների ծածկագրման ամենահայտնի կիրառություններից երկուսն են.

  • Հանրային բանալիով գաղտնագրում, որի դեպքում հաղորդագրությունը կոդավորված է նախատեսված ստացողի հանրային բանալիով։ Պատշաճ ընտրված և օգտագործված ալգորիթմների դեպքում հաղորդագրությունները գործնականում չեն կարող վերծանվել որևէ մեկի կողմից, ով չունի համապատասխան անձնական բանալի, ով, հետևաբար, ենթադրվում է, որ այդ բանալիի սեփականատերն է և, հետևաբար, հանրային բանալու հետ կապված անձը։ Սա կարող է օգտագործվել հաղորդագրության գաղտնիությունն ապահովելու համար[7]։
  • Թվային ստորագրություններ, որոնցում հաղորդագրությունը ստորագրվում է ուղարկողի անձնական բանալիով և կարող է ստուգվել յուրաքանչյուրի կողմից, ով մուտք ունի ուղարկողի հանրային բանալին։ Այս ստուգումն ապացուցում է, որ ուղարկողն ուներ մուտք դեպի մասնավոր բանալին, և, հետևաբար, շատ հավանական է, որ նա լինի հանրային բանալու հետ կապված անձը։ Սա նաև ապացուցում է, որ ստորագրությունը պատրաստվել է հենց այդ հաղորդագրության համար, քանի որ ստուգումը չի հաջողվի ցանկացած այլ հաղորդագրության համար, որը կարելի է ստեղծել առանց անձնական բանալի օգտագործելու։

Կարևոր խնդիր է վստահությունը/ապացույցն այն մասին, որ որոշակի հանրային բանալին իսկական է, այսինքն՝ այն ճիշտ է և պատկանում է հայցվող անձին կամ կազմակերպությանը, և այն չի կեղծվել կամ փոխարինվել որևէ (հնարավոր է, չարամիտ) երրորդ կողմի կողմից։ Կան մի քանի հնարավոր մոտեցումներ, այդ թվում՝

Հանրային բանալիների ենթակառուցվածք (PKI), որտեղ մեկ կամ մի քանի երրորդ կողմեր, որոնք հայտնի են որպես վկայականի մարմիններ, հավաստում են բանալիների զույգերի սեփականությունը։ TLS-ը հենվում է դրա վրա։ Սա ենթադրում է, որ PKI համակարգը (ծրագրային ապահովում, սարքավորում և կառավարում) վստահելի է բոլոր ներգրավվածների կողմից։

«Վստահության վեբ», որն ապակենտրոնացնում է նույնականացումը՝ օգտագործելով օգտատիրոջ և այդ օգտատիրոջը պատկանող հանրային բանալիների միջև կապերի անհատական հաստատումները։ PGP-ն օգտագործում է այս մոտեցումը՝ ի լրումն տիրույթի անունների համակարգում (DNS) որոնումների։ Նամակների թվային ստորագրման DKIM համակարգը նույնպես օգտագործում է այս մոտեցումը։

Դիմումներ

խմբագրել

Հանրային բանալիների գաղտնագրման համակարգի առավել ակնհայտ կիրառումը հաղորդակցության գաղտնագրումն է` գաղտնիություն ապահովելու համար։ Հաղորդագրություն, որը ուղարկողը գաղտնագրում է` օգտագործելով ստացողի հանրային բանալին, որը կարող է վերծանվել միայն ստացողի զուգակցված մասնավոր բանալիով։

Հանրային բանալիների ծածկագրության մեկ այլ կիրառություն թվային ստորագրությունն է։ Թվային ստորագրության սխեմաները կարող են օգտագործվել ուղարկողի իսկությունը հաստատելու համար։

Ոչ մերժման համակարգերը օգտագործում են թվային ստորագրություններ՝ երաշխավորելու, որ կողմերից մեկը չի կարող հաջողությամբ վիճարկել փաստաթղթի կամ հաղորդակցության իր հեղինակությունը։

Այս հիմքի վրա կառուցված հետագա հավելվածները ներառում են թվային կանխիկ գումար, գաղտնաբառով վավերացված բանալի համաձայնագիր, ժամանակի դրոշմավորման ծառայություններ և չհրաժարման արձանագրություններ։

Հիբրիդային կրիպտոհամակարգեր

խմբագրել

Քանի որ ասիմետրիկ բանալիների ալգորիթմները գրեթե միշտ շատ ավելի ինտենսիվ են, քան սիմետրիկները, սովորական է օգտագործել հանրային/մասնավոր ասիմետրիկ բանալիների փոխանակման ալգորիթմ՝ սիմետրիկ բանալի գաղտնագրելու և փոխանակելու համար, որն այնուհետև օգտագործվում է սիմետրիկ բանալի կրիպտոգրաֆիայի միջոցով՝ տվյալների փոխանցման համար այժմ համօգտագործվող սիմետրիկ բանալին սիմետրիկ բանալիների կոդավորման ալգորիթմի համար։ PGP, SSH և SSL/TLS սխեմաների ընտանիքն օգտագործում են այս ընթացակարգը. Այսպիսով, դրանք կոչվում են հիբրիդային կրիպտոհամակարգեր։ Նախնական ասիմետրիկ կրիպտոգրաֆիայի վրա հիմնված բանալիների փոխանակումը՝ սերվերի կողմից ստեղծված սիմետրիկ բանալիով սերվերից հաճախորդին համօգտագործելու համար, ունի առավելություն, որ չի պահանջում, որ սիմետրիկ բանալին նախապես համօգտագործվի ձեռքով, օրինակ՝ տպագիր թղթի վրա կամ սուրհանդակով տեղափոխվող սկավառակների վրա, միևնույն ժամանակ ապահովելով սիմետրիկ բանալիների կրիպտոգրաֆիայի տվյալների ավելի բարձր թողունակությունը, քան ասիմետրիկ բանալիների ծածկագրումը ընդհանուր կապի մնացած մասի համար։

Թույլ կողմեր

խմբագրել

Ինչպես անվտանգության հետ կապված բոլոր համակարգերում, կարևոր է բացահայտել հնարավոր թույլ կողմերը։ Բացի ասիմետրիկ բանալիների ալգորիթմի վատ ընտրությունից (քչերն են, որոնք լայնորեն համարվում են բավարար) կամ բանալու չափազանց կարճ երկարությունից, անվտանգության գլխավոր ռիսկն այն է, որ հայտնի է դառնում զույգի մասնավոր բանալին։ Հաղորդագրությունների ողջ անվտանգությունը, նույնականացումը և այլն, այնուհետև կկորչեն։

Ալգորիթմներ

խմբագրել

Հանրային բանալիների բոլոր սխեմաները տեսականորեն ենթակա են «կոպիտ ուժային բանալիների որոնման հարձակման»[8]։ Այնուամենայնիվ, նման հարձակումն անիրագործելի է, եթե հաջողության հասնելու համար անհրաժեշտ հաշվարկների քանակը, որը Կլոդ Շենոնի կողմից կոչվում է «աշխատանքային գործոն», անհասանելի է բոլոր պոտենցիալ հարձակվողներին։ Շատ դեպքերում աշխատանքի գործոնը կարող է մեծանալ՝ պարզապես ընտրելով ավելի երկար բանալի։ Բայց այլ ալգորիթմները կարող են ի սկզբանե ունենալ շատ ավելի ցածր աշխատանքային գործոններ, ինչը անտեղի է դարձնում բիրտ ուժի հարձակման դիմադրությունը (օրինակ՝ ավելի երկար ստեղներից)։ Որոշ հատուկ և կոնկրետ ալգորիթմներ են մշակվել՝ օգնելու գրոհել հանրային բանալիների գաղտնագրման ալգորիթմները։ Եվ՛ RSA, և՛ ElGamal կոդավորումները հայտնի են հարձակումներ, որոնք շատ ավելի արագ են, քան բիրտ ուժի մոտեցումը[9]։ Սրանցից ոչ մեկը բավականաչափ բարելավված չէ, որպեսզի իրականում գործնական լինի։

Հիմնական թույլ կողմերը հայտնաբերվել են նախկինում խոստումնալից ասիմետրիկ հիմնական ալգորիթմների համար։ Նոր հարձակման մշակումից հետո պարզվել է, որ «պայուսակի փաթեթավորման» ալգորիթմը անապահով է[10]։ Ինչպես բոլոր կրիպտոգրաֆիկ գործառույթների դեպքում, հանրային բանալիների իրականացումը կարող է խոցելի լինել կողմնակի ալիքի հարձակումների համար, որոնք օգտագործում են տեղեկատվության արտահոսքը՝ պարզեցնելու գաղտնի բանալի որոնումը։ Սրանք հաճախ անկախ են օգտագործվող ալգորիթմից։ Հետազոտություններ են իրականացվում ինչպես հայտնաբերելու, այնպես էլ նոր հարձակումներից պաշտպանվելու համար։

Հանրային բանալիների փոփոխություն

խմբագրել

Ասիմետրիկ բանալիների օգտագործման մեկ այլ պոտենցիալ անվտանգության խոցելիություն է «մարդը միջինում» հարձակման հնարավորությունը, որտեղ հանրային բանալիների հաղորդակցությունը գաղտնալսվում է երրորդ կողմի կողմից («մարդը միջինում») և այնուհետև փոփոխվում է՝ փոխարենը տարբեր հանրային բանալիներ տրամադրելու համար։ Գաղտնագրված հաղորդագրությունները և պատասխանները պետք է բոլոր դեպքերում գաղտնալսվեն, վերծանվեն և վերակոդավորվեն հարձակվողի կողմից՝ օգտագործելով հաղորդակցության տարբեր հատվածների ճիշտ հանրային բանալիները, որպեսզի խուսափեն կասկածներից։

Ասում են, որ հաղորդակցությունն անապահով է, երբ տվյալները փոխանցվում են այնպես, որ թույլ է տալիս գաղտնալսել (նաև կոչվում է «sniffing»): Այս պայմանները վերաբերում են ուղարկողի անձնական տվյալների ամբողջական ընթերցմանը։ Հաղորդակցությունը հատկապես վտանգավոր է, երբ գաղտնալսումները չեն կարող կանխվել կամ վերահսկվել ուղարկողի կողմից[11]։

«Մարդը միջինում» հարձակումը կարող է դժվար լինել իրականացնել ժամանակակից անվտանգության արձանագրությունների բարդությունների պատճառով։ Այնուամենայնիվ, խնդիրն ավելի պարզ է դառնում, երբ ուղարկողը օգտագործում է անապահով լրատվամիջոցներ, ինչպիսիք են հանրային ցանցերը, ինտերնետը կամ անլար կապը: Այս դեպքերում հարձակվողը կարող է վտանգի ենթարկել կապի ենթակառուցվածքը, այլ ոչ թե բուն տվյալները։ Ինտերնետ Ծառայությունների Մատակարարի (ISP) հիպոթետիկ չարամիտ աշխատակիցը կարող է համեմատաբար պարզ համարել «մարդ-միջին» հարձակումը։ Հանրային բանալին գրավելու համար կպահանջվի միայն որոնել բանալին, քանի որ այն ուղարկվում է ISP-ի հաղորդակցման սարքաշարի միջոցով։ Պատշաճ կերպով իրականացվող ասիմետրիկ բանալիների սխեմաներում դա էական ռիսկ չէ։

Որոշ առաջադեմ «մարդ-միջին» հարձակումների դեպքում հաղորդակցության մի կողմը կտեսնի բնօրինակ տվյալները, իսկ մյուս կողմը կստանա վնասակար տարբերակ։ Ասիմետրիկ «մարդ-միջին» հարձակումները կարող են խանգարել օգտվողներին գիտակցել, որ իրենց կապը վտանգված է։ Սա մնում է այդպես, նույնիսկ այն դեպքում, երբ հայտնի է, որ մի օգտագործողի տվյալները վտանգված են, քանի որ տվյալները մյուս օգտատիրոջը լավ են թվում։ Սա կարող է հանգեցնել օգտատերերի միջև շփոթեցնող տարաձայնությունների, ինչպիսիք են՝ «դա պետք է լինի ձեր վերջում»․ երբ օգտատերերից ոչ մեկը մեղավոր չէ։ Հետևաբար, «մարդը միջինում» հարձակումները լիովին կանխարգելելի են միայն այն դեպքում, երբ հաղորդակցության ենթակառուցվածքը ֆիզիկապես վերահսկվում է կողմերից մեկի կամ երկուսի կողմից. օրինակ՝ լարային երթուղու միջոցով՝ ուղարկողի սեփական շենքի ներսում։ Ընդհանուր առմամբ, հանրային բանալիներն ավելի հեշտ են փոփոխվում, երբ ուղարկողի կողմից օգտագործվող հաղորդակցման սարքավորումը վերահսկվում է հարձակվողի կողմից[12][13][14]։

Հանրային բանալի ենթակառուցվածք

խմբագրել

Նման հարձակումները կանխելու մոտեցումներից մեկը ներառում է հանրային բանալին ենթակառուցվածքի (PKI) օգտագործումը. մի շարք դերեր, քաղաքականություններ և ընթացակարգեր, որոնք անհրաժեշտ են թվային վկայագրերը ստեղծելու, կառավարելու, տարածելու, օգտագործելու, պահելու և չեղյալ համարելու և հանրային բանալիների կոդավորումը կառավարելու համար։ Այնուամենայնիվ, սա պոտենցիալ թույլ կողմեր ունի։

Օրինակ՝ վկայականը տվող սերտիֆիկատի մարմինը պետք է վստահի բոլոր մասնակից կողմերին, որ պատշաճ կերպով ստուգել է բանալիատիրոջ ինքնությունը, ապահովել է հանրային բանալու ճիշտությունը վկայագիր տրամադրելիս, պաշտպանված լինել համակարգչային ծովահենությունից, և բոլոր մասնակիցների հետ պայմանավորվել՝ ստուգելու նրանց բոլոր վկայականները, նախքան պաշտպանված հաղորդակցությունները սկսելը։ Վեբ բրաուզերներին, օրինակ, տրամադրվում է «ինքնաստորագրված ինքնության վկայականների» երկար ցուցակ PKI պրովայդերներից։ Դրանք օգտագործվում են սերտիֆիկատների երեսի բարեխիղճությունը ստուգելու համար, այնուհետև, երկրորդ քայլում, պոտենցիալ հաղորդակցողների վկայականները։ Հարձակվողը, ով կարող է տապալել այդ սերտիֆիկատներից որևէ մեկին կեղծ հանրային բանալու համար վկայագիր տալու համար, կարող է այնուհետև «մարդը միջինում» հարձակում գործել այնքան հեշտությամբ, կարծես վկայագրի սխեման ընդհանրապես չի օգտագործվել։ Հազվադեպ քննարկվող այլընտրանքային սցենարում հարձակվողը, ով ներթափանցում է իշխանության սերվերներ և ստանում դրա վկայականների և բանալիների պահեստը (հանրային և մասնավոր), կարող է անսահմանափակ կեղծել, վերծանել և կեղծել գործարքները։

Չնայած իր տեսական և պոտենցիալ խնդիրներին՝ այս մոտեցումը լայնորեն կիրառվում է։ Օրինակները ներառում են TLS-ը և նրա նախորդ SSL-ը, որոնք սովորաբար օգտագործվում են վեբ բրաուզերի գործարքների անվտանգությունն ապահովելու համար (օրինակ՝ կրեդիտ քարտի տվյալները առցանց խանութին անվտանգ ուղարկելու համար)։

Բացի որոշակի բանալիների զույգի հարձակման դիմադրությունից, հանրային բանալիների համակարգերը տեղակայելիս պետք է հաշվի առնել սերտիֆիկացման հիերարխիայի անվտանգությունը։ Որոշ սերտիֆիկատներ (սովորաբար հատուկ կառուցված ծրագիր, որն աշխատում է սերվերային համակարգչի վրա), երաշխավորում են որոշակի մասնավոր բանալիների ինքնությունը՝ արտադրելով թվային վկայագիր։ Հանրային բանալիների թվային վկայագրերը սովորաբար վավեր են մի քանի տարի միաժամանակ, ուստի հարակից մասնավոր բանալիները պետք է ապահով պահվեն այդ ընթացքում։ Երբ PKI սերվերի հիերարխիայում ավելի բարձր վկայագրի ստեղծման համար օգտագործվող մասնավոր բանալին վտանգված է կամ պատահաբար բացահայտվում է, ապա հնարավոր է «մարդը միջին գրոհ»՝ ցանկացած ենթակա վկայական դարձնելով լիովին անապահով։

Օրինակներ

խմբագրել

Տարբեր նպատակների համար լավ դիտարկված ասիմետրիկ հիմնական տեխնիկայի օրինակները ներառում են.

Ասիմետրիկ հիմնական ալգորիթմների օրինակները, որոնք դեռ լայնորեն չեն ընդունվել, ներառում են.

Հատկանշական, բայց ոչ անվտանգ, ասիմետրիկ հիմնական ալգորիթմների օրինակները ներառում են.

Ասիմետրիկ բանալիների ալգորիթմներ օգտագործող արձանագրությունների օրինակները ներառում են.

Պատմություն

խմբագրել

Կրիպտոգրաֆիայի վաղ պատմության ընթացքում երկու կողմերը ապավինում էին բանալիին, որը նրանք կփոխանակեին ապահով, բայց ոչ գաղտնագրային մեթոդի միջոցով, ինչպիսին է դեմ առ դեմ հանդիպումը կամ վստահելի սուրհանդակը։ Այս բանալին, որն այնուհետև երկու կողմերը պետք է բացարձակապես գաղտնի պահեն, կարող են օգտագործվել կոդավորված հաղորդագրություններ փոխանակելու համար։ Բանալիների բաշխման այս մոտեցմամբ առաջանում են մի շարք նշանակալի գործնական դժվարություններ։

Ակնկալիք

խմբագրել

Իր 1874 թվականի «Գիտության սկզբունքները» գրքում Ուիլյամ Սթենլի Ջևոնս[15] գրել է՝

Ընթերցողը կարո՞ղ է ասել, թե ինչ երկու թվերի հետ բազմապատկելով կստացվի 8616460799 թիվը[16]։ Ես քիչ հավանական եմ համարում, որ ինձնից բացի որևէ մեկը երբևէ իմանա[17]։

Այստեղ նա նկարագրեց միակողմանի ֆունկցիաների կապը գաղտնագրության հետ և շարունակեց քննարկել հատկապես ֆակտորիզացիայի խնդիրը, որն օգտագործվում էր trapdoor ֆունկցիա ստեղծելու համար։ 1996 թվականի հուլիսին մաթեմատիկոս Սոլոմոն Վ. Գոլոմբն ասաց. «Ջևոնսը ակնկալում էր RSA ալգորիթմի հիմնական առանձնահատկությունը հանրային բանալիների ծածկագրման համար, թեև նա, անշուշտ, չէր հորինել հանրային բանալիների գաղտնագրության գաղափարը»[18]։

Դասակարգված բացահայտում

խմբագրել

1970 թվականին Ջեյմս Հ. Էլլիսը՝ բրիտանացի կրիպտոգրաֆը, Միացյալ Թագավորության Կառավարության Հաղորդակցման Գլխավոր գրասենյակում (GCHQ) հասկացավ «ոչ գաղտնի գաղտնագրման» հնարավորությունը (այժմ կոչվում է հանրային բանալի կրիպտոգրաֆիա), բայց չկարողացավ տեսնել այն իրականացնելու հնարավորությունը[19][20]։ 1973 թվականին նրա գործընկեր Քլիֆորդ Քոքսը ներդրեց այն, ինչը հայտնի դարձավ որպես RSA կոդավորման ալգորիթմ՝ տալով «ոչ գաղտնի գաղտնագրման» գործնական մեթոդ, իսկ 1974 թվականին GCHQ-ի մեկ այլ մաթեմատիկոս և կրիպտոգրաֆ Մալքոլմ Ջ. Ուիլյամսոնը մշակեց այն, ինչ այժմ հայտնի է որպես Diffie-Hellman բանալիների փոխանակում։ Սխեման փոխանցվել է նաև ԱՄՆ Ազգային անվտանգության գործակալությանը[21]։ Երկու կազմակերպություններն էլ ունեին ռազմական ուղղվածություն և ամեն դեպքում հասանելի էր միայն սահմանափակ հաշվողական հզորությունը։ Հանրային բանալիների գաղտնագրության ներուժը մնացել է չիրացված ոչ մի կազմակերպության կողմից։

Ես դա համարում էի ամենակարևորը ռազմական օգտագործման համար... եթե դուք կարողանաք արագ և էլեկտրոնային եղանակով կիսել ձեր բանալին, դուք մեծ առավելություն ունեք ձեր հակառակորդի նկատմամբ։ Միայն էվոլյուցիայի վերջում Բերներս-Լիի կողմից CERN-ի համար բաց ինտերնետային ճարտարապետություն նախագծելը, դրա հարմարեցումը և ընդունումը Arpanet-ի համար… արդյո՞ք հանրային բանալի գաղտնագրությունն իրացրել է իր ողջ ներուժը։

Ռալֆ Բենջամին[21]

Այս հայտնագործությունները հրապարակայնորեն չճանաչվեցին 27 տարի, մինչև որ հետազոտությունը գաղտնազերծվեց բրիտանական կառավարության կողմից 1997թվականին[22]։

Հասարակական բացահայտում

խմբագրել

1976 թվականին ասիմետրիկ բանալիների կրիպտոհամակարգը հրապարակվեց Ուիթֆիլդ Դիֆիի և Մարտին Հելմանի կողմից, ովքեր, ազդվելով հանրային բանալիների բաշխման վերաբերյալ Ռալֆ Մերկլի աշխատանքից, բացահայտեցին հանրային բանալիների համաձայնության մեթոդը։ Բանալինների փոխանակման այս մեթոդը, որն օգտագործում է ուժգնացում վերջավոր դաշտում, հայտնի դարձավ որպես Դիֆի–Հելման բանալիների փոխանակում[23]։ Սա առաջին հրապարակված գործնական մեթոդն էր՝ հաստատված (բայց ոչ գաղտնի) կապի ալիքի վրա ընդհանուր գաղտնի բանալի ստեղծելու համար՝ առանց նախնական ընդհանուր գաղտնիքի օգտագործման։ Մերկլի «հանրային բանալիների համաձայնագրի տեխնիկան» հայտնի դարձավ որպես Մերկլի հանելուկներ և հայտնագործվեց 1974 թվականին և հրապարակվեց միայն 1978 թվականին։ Սա ասիմետրիկ գաղտնագրումը դարձնում է բավականին նոր ոլորտ գաղտնագրության մեջ, թեև կրիպտոգրաֆիան ինքնին ավելի քան 2000 տարվա վաղեմություն ունի[24]։

1977 թվականին Քոքսի սխեմայի ընդհանրացումն ինքնուրույն հորինել են Ռոն Ռիվեստը, Ադի Շամիրը և Լեոնարդ Ադլեմանը, այնուհետև MIT-ում։ Վերջին հեղինակները հրապարակել են իրենց աշխատանքը 1978 թվականին Մարտին Գարդների «Scientific American» ամսագրում, և ալգորիթմը հայտնի է դարձել որպես RSA՝ իրենց անունների սկզբնատառերից[25]։ RSA-ն օգտագործում է հզորացման մոդուլ երկու շատ մեծ պարզ թվերի արտադրանք գաղտնագրելու և վերծանելու համար՝ կատարելով և՛ հանրային բանալիների կոդավորումը, և՛ հանրային բանալիների թվային ստորագրությունները։ Դրա անվտանգությունը կապված է մեծ ամբողջ թվերի ֆակտորինգի ծայրահեղ դժվարության հետ, խնդիր, որի համար հայտնի արդյունավետ ընդհանուր տեխնիկա չկա (չնայած սկզբնական ֆակտորիզացիան կարելի է ձեռք բերել բիրտ ուժի գրոհների միջոցով. որքան մեծանում են հիմնական գործոնները, դա շատ ավելի դժվար է դառնում)։ Ալգորիթմի նկարագրությունը հրապարակվել է «Mathematical Games» ամսագրում՝ Scientific American-ի 1977 թվականի օգոստոսի համարում[26]։

1970-ականներից ի վեր մշակվել են գաղտնագրման, թվային ստորագրության, բանալիների համաձայնեցման և այլ տեխնիկայի մեծ քանակություն և բազմազանություն, ներառյալ Rabin կրիպտոհամակարգը, ElGamal ծածկագրումը, DSA - և էլիպսային կորի ծածկագրումը։

Ծանոթագրություններ

խմբագրել
  1. ↑ Bernstein, Daniel J.; Lange, Tanja (2017 թ․ սեպտեմբերի 14). «Post-quantum cryptography». Nature (անգլերեն). 549 (7671): 188–194. Bibcode:2017Natur.549..188B. doi:10.1038/nature23461. ISSN 0028-0836. PMID 28905891. S2CID 4446249.
  2. ↑ Stallings, William (1990 թ․ մայիսի 3). Cryptography and Network Security: Principles and Practice (անգլերեն). Prentice Hall. էջ 165. ISBN 9780138690175.
  3. ↑ Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (1996 թ․ հոկտեմբեր). «8: Public-key encryption». Handbook of Applied Cryptography (PDF). CRC Press. էջեր 283–319. ISBN 0-8493-8523-7. Վերցված է 2022 թ․ հոկտեմբերի 8-ին.
  4. ↑ Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (1996 թ․ հոկտեմբեր). «8: Public-key encryption». Handbook of Applied Cryptography (PDF). CRC Press. էջեր 425–488. ISBN 0-8493-8523-7. Վերցված է 2022 թ․ հոկտեմբերի 8-ին.
  5. ↑ Bernstein, Daniel J. (2008 թ․ մայիսի 1). «Protecting communications against forgery». Algorithmic Number Theory (PDF). Vol. 44. MSRI Publications. §5: Public-key signatures, pp. 543-545. Վերցված է 2022 թ․ հոկտեմբերի 8-ին.
  6. ↑ Alvarez, Rafael; Caballero-Gil, Cándido; Santonja, Juan; Zamora, Antonio (2017 թ․ հունիսի 27). «Algorithms for Lightweight Key Exchange». Sensors (անգլերեն). 17 (7): 1517. doi:10.3390/s17071517. ISSN 1424-8220. PMC 5551094. PMID 28654006.
  7. ↑ «Asymmetric encryption». IONOS Digitalguide (անգլերեն). Վերցված է 2022 թ․ հունիսի 2-ին.
  8. ↑ Paar, Christof; Pelzl, Jan; Preneel, Bart (2010). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. ISBN 978-3-642-04100-6.
  9. ↑ Mavroeidis, Vasileios, and Kamer Vishi, "The Impact of Quantum Computing on Present Cryptography", International Journal of Advanced Computer Science and Applications, 31 March 2018
  10. ↑ Shamir, Adi (1982 թ․ նոյեմբեր). «A polynomial time algorithm for breaking the basic Merkle-Hellman cryptosystem». 23rd Annual Symposium on Foundations of Computer Science (SFCS 1982): 145–152. doi:10.1109/SFCS.1982.5.
  11. ↑ Tunggal, Abi (2020 թ․ փետրվարի 20). «What Is a Man-in-the-Middle Attack and How Can It Be Prevented - What is the difference between a man-in-the-middle attack and sniffing?». UpGuard. Վերցված է 2020 թ․ հունիսի 26-ին.
  12. ↑ Tunggal, Abi (2020 թ․ փետրվարի 20). «What Is a Man-in-the-Middle Attack and How Can It Be Prevented - Where do man-in-the-middle attacks happen?». UpGuard. Վերցված է 2020 թ․ հունիսի 26-ին.
  13. ↑ martin (2013 թ․ հունվարի 30). «China, GitHub and the man-in-the-middle». GreatFire. Արխիվացված օրիգինալից 2016 թ․ օգոստոսի 19-ին. Վերցված է 2015 թ․ հունիսի 27-ին.
  14. ↑ percy (2014 թ․ սեպտեմբերի 4). «Authorities launch man-in-the-middle attack on Google». GreatFire. Վերցված է 2020 թ․ հունիսի 26-ին.
  15. ↑ Jevons, William Stanley, The Principles of Science: A Treatise on Logic and Scientific Method p. 141, Macmillan & Co., London, 1874, 2nd ed. 1877, 3rd ed. 1879. Reprinted with a foreword by Ernst Nagel, Dover Publications, New York, NY, 1958.
  16. ↑ This came to be known as "Jevons's number". The only nontrivial factor pair is 89681 × 96079.
  17. ↑ Principles of Science, Macmillan & Co., 1874, p. 141.
  18. ↑ Golob, Solomon W. (1996). «On Factoring Jevons' Number». Cryptologia. 20 (3): 243. doi:10.1080/0161-119691884933. S2CID 205488749.
  19. ↑ Ellis, James H. (1970 թ․ հունվար). «THE POSSIBILITY OF SECURE NON-SECRET DIGITAL ENCRYPTION» (PDF). {{cite journal}}: Cite journal requires |journal= (օգնություն)
  20. ↑ Sawer, Patrick (2016 թ․ մարտի 11). «The unsung genius who secured Britain's computer defences and paved the way for safe online shopping». The Telegraph.
  21. ↑ 21,0 21,1 Espiner, Tom (2010 թ․ հոկտեմբերի 26). «GCHQ pioneers on birth of public key crypto». www.zdnet.com.
  22. ↑ Singh, Simon (1999). The Code Book. Doubleday. էջեր 279–292.
  23. ↑ Diffie, Whitfield; Hellman, Martin E. (1976 թ․ նոյեմբեր). «New Directions in Cryptography» (PDF). IEEE Transactions on Information Theory. 22 (6): 644–654. CiteSeerX 10.1.1.37.9720. doi:10.1109/TIT.1976.1055638. Արխիվացված (PDF) օրիգինալից 2014 թ․ նոյեմբերի 29-ին.
  24. ↑ «Asymmetric encryption». IONOS Digitalguide (անգլերեն). Վերցված է 2022 թ․ հունիսի 9-ին.
  25. ↑ Rivest, R.; Shamir, A.; Adleman, L. (1978 թ․ փետրվար). «A Method for Obtaining Digital Signatures and Public-Key Cryptosystems» (PDF). Communications of the ACM. 21 (2): 120–126. CiteSeerX 10.1.1.607.2677. doi:10.1145/359340.359342. S2CID 2873616. Արխիվացված է օրիգինալից (PDF) 2008 թ․ դեկտեմբերի 17-ին. Վերցված է 2023 թ․ մայիսի 2-ին.
  26. ↑ Robinson, Sara (2003 թ․ հունիս). «Still Guarding Secrets after Years of Attacks, RSA Earns Accolades for its Founders» (PDF). SIAM News. 36 (5). Արխիվացված է օրիգինալից (PDF) 2017 թ․ հունվարի 16-ին. Վերցված է 2023 թ․ մայիսի 2-ին.

Գրականություն

խմբագրել

Արտաքին հղումներ

խմբագրել
 Վիքիպահեստն ունի նյութեր, որոնք վերաբերում են «Հանրային բանալիների գաղտնագրություն» հոդվածին։
Ստացված է «https://hy.wiki.x.io/w/index.php?title=Հանրային_բանալիների_գաղտնագրություն&oldid=9717238» էջից